Laplace's Equation
Laplace's equation describes a wide variety of problems of physics and engineering
- Diffusion of fluid in a porois media, Temperature distribution, Electrostatics,
Magnetostatics among others. In two dimensions, it has the form
-c(uxx + uyy)
= f(x,y)
with Dirichlet boundary condition
u = u0
on the boundary.
Alternatively, one can specify Neumann boundary conditions
Pressure distributuion in an annulus
Consider two concentric circles - the inner one has radius r0
and the outer one radius r1. The general
axisymmetric solution of the problem in two dimensionsis, without a forcing
term, that is f(x,y) = 0 is of the form:
u = C1
r+C2/r ,
where C1 and C2
are two constants that can be detwrmined from the boundary conditions.
Since an anlytic solution is available, it is convenient to use and test
the correctness of the FEM solution. The problem is solved numerically with
r0=0.01 and r1
= 1. On the inner circle, u = 1 and on the outer circle u = 0,
which implies C1 = -C2
= 100/9999. A multigrid method was used, with the the initial
mesh shown on the next figure.
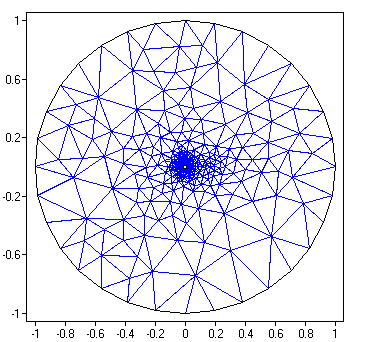
Click on image to see the sequences of meshes used in the multigrid solver
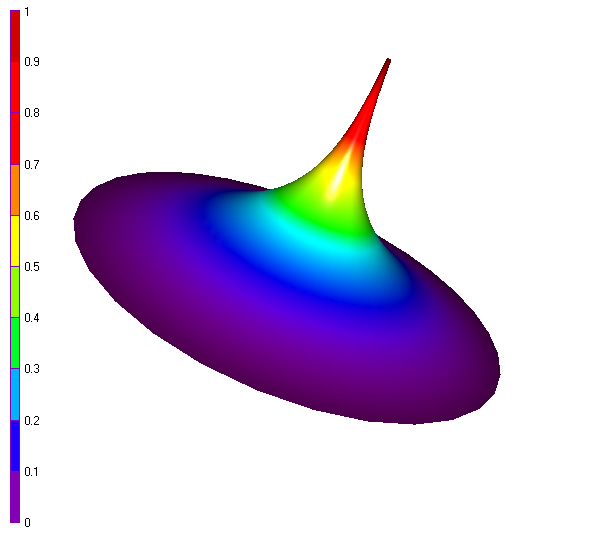
Surface plot of the solution on the finest mesh (~123 000 degrees of freedom)
After appropriate scaling to nondimensional variables, this solution can
be interpreted as the pressure distribution away from a cylindrical well,
the electrostatic potential between a charged inner cylinder and a grounded
outer cylinder or the radial displacement in a pressurized elastic cylinder.
Plate Capacitor
This is a problem
for a 2D plate capacitor and was given as homework in the class "Introduction to scientific
computing" at the math department
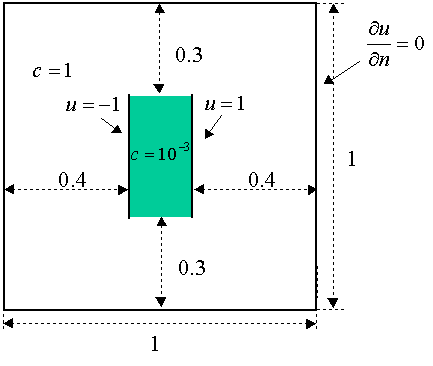
at Texas A&M University. The schematic of
the capacitor is shown on the next figure. The green area correspondes to
an isolator, i.e. material with low electric conductivity and the rest of
the domain is taken by a higher conductivity medium.
For some reason, this problem results in a really nice surface plot for
the electric potenrial. The solution is plotted on the next three graphs.
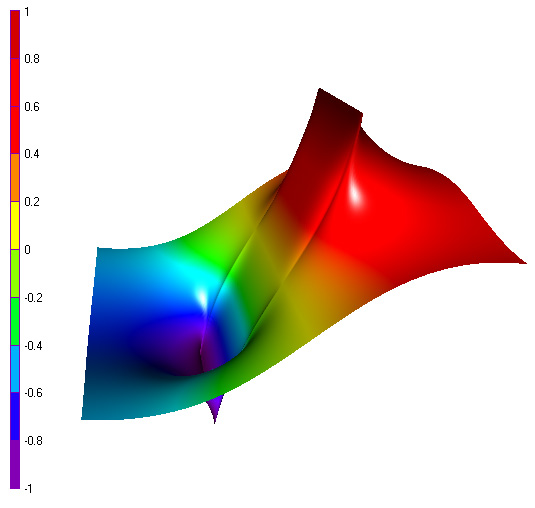
Surface plot of the electric potential
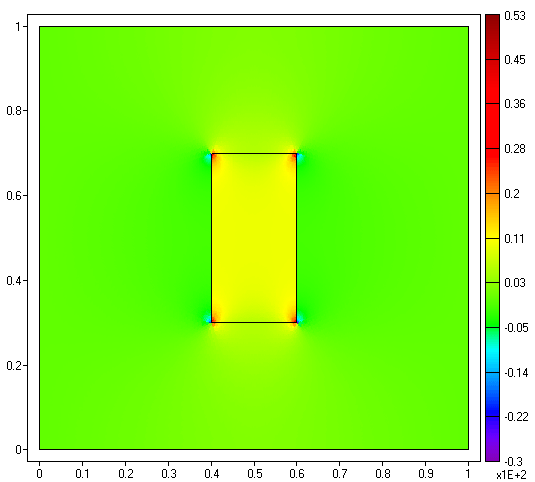
Contour plot of the x-component of the electric field (E1
= ux)
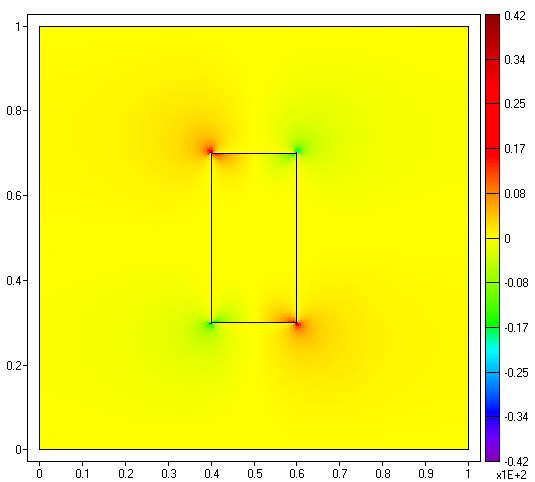
Contour plot of the y-component of the electric field (E2
= uy)





